Мамедов Джаббар Манаф оглы
[Азербайджан]
НОВАЯ ИНТЕРПРЕТАЦИЯ «ЭФФЕКТА ХАББЛА»
|
ИЗДАТЕЛИ:
|
Работа является отрывком из книги автора “Заметки и замечания, относительно ряда базовых принципов современной физической науки”, Баку, 1999, пер. на русскую Баку, 2005; см.: 4;
Журнал “Знание”, Серия “Технические науки” №1, Баку, 2005
Международный журнал экспериментального образования (ISSN - 1996-3947). #9. 2010
|
|
РЕЦЕНЗЕНТЫ
|
Факультет Физики Азерб.Гос.Пед.Университета
Некоторые индивидуальные рецензий
|
|
СКАЧАТЬ
|
Скачать только эту часть
Скачать всю работу
|
|
АДРЕС МАТЕРИАЛА В ИНТЕРНЕТЕ
|
http://www.phillaw.aznet.org/monru/physic/bigbang_ru.htm
http://j-m-mamedov.narod.ru/russian/physic/bigbang_ru.htm
|
|
ФОРУМ, ГДЕ ОБСУЖДАЕТСЯ ЭТА РАБОТА
|
http://www.astronomy.ru/forum/index.phr/topic,10650.0.html
|
...Как известно, "эффект Хаббл"а имеет нескольких интерпретаций, исходя из разных концепций. Некоторые из них следующие:
— Первая версия (стандартная модель “Большого взрыва”. Опирается на Фридмановские решений Эйнштейновых формул): Вся масса вселенной когда-то локализовалась в одной точке и после какого-то момента (взрыва) вся эта масса начала разлетать (причина взрыва пока остается спорным);
— Вторая версия (гипотеза о “старении” света): при распространении на далекие расстояния, просто световые волны теряют энергию и частично затухаются;
— Третья версия (гипотеза об изменение плотности пространства за миллиарды лет): Приходящий к нам сегодня от далеких галактик “красносмещенный” свет, был излучен миллиарды лет назад в пространство с другими свойствами (с большей плотностью), поэтому его “красное смещение” объясняется вовсе не доплеровским эффектом, а “возрастом” света (О. Эстерле, 1992). Со временам плотности эфира уменьшался, по причине того, что массивные тела “ожирели его”: но нам доходящий этот “красно смещенный” свет, был излучен в его более плотном же этапе;
— Четвертую версию (оптическую) мы выдвигаем здесь, короткое содержание, которой состоит из следующего: В своей книге мы сталкивались с таким эффектом: допустим к нам приближаются 10 объектов и столько же удаляются. Поскольку мы фиксируем всех их через ЭМ.-волны, а скорость этих волн являются не бесконечными, получается, что расстояния между этими объектами будут проецироваться в наблюдательный пункт отличным от реального. По точнее, расстояние между удаляющимся будет казаться больше, а между приближающимся – меньше реального. И еще: как известно, мы сможем наблюдать не всю вселенную в целом, а только ее ту часть которая находится внутри определенной горизонта видимости. Объекты находящийся вне этого горизонта видимости нам недоступно, т.к. сигналы от них пока нам не доходили. Но оказывается и здесь асимметрия: из вычислений получается, что горизонт видимости приближающихся тел не совпадает с горизонтом видимости удаляющихся тел. Т.к. поскольку удаляющийся объект когда то был ближе к нам, мы успевали фиксировать и прежнюю и нынешнюю местоположению его. А приближающийся только, что переходил эту черту, поэтому его прежние состояний нам неизвестны. Итак, получается, что мы обладаем информацией о всех удаляющихся, а только о части приближающихся объектов. Отсюда и красное смещение: чем дальше, тем меньше фиксируются приближающие. А после определенного горизонта мы вообще не в силе фиксировать приближающихся, но удаляющиеся фиксируются еще долго. И как сказали выше, у них длина волн смешен к красную область. Получается, что после определенной точки, мы будем наблюдать только красносмещенных объектов.
Итого, "расширение вселенной" не более чем оптическая иллюзия, обусловленная принципом близкодействия. Это кажущееся расширение, а не действительное. Реальная стационарность вселенной в любом варианте проецируется на человеческие восприятия динамичным. Эта версия принадлежит нам. Более расщиренно эту версию излагаем внизу.
Представьте самолет, летящий к вам со скоростью V=1/2U, где V – скорость самолета и U – скорость звука. На пути, на равном расстоянии друг от друга расположены, 5 пунктов. Дистанция между ними равна 1Ut, т.е. столько, сколько звук преодолевает за одну секунду. Итого последний находится на расстоянии 5Ut от вас. Допустим, вы определяете время прибытия самолета в каждый пункт через звуковой сигнал, отправленный из него при прибытии в каждый пункт. Время прибытия и время фиксации этого прибытия будет таким:
| x |
x5 |
x4 |
x3 |
x2 |
x1 |
x0 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.05 |
00.06 |
00.07 |
00.08 |
00.09 |
00.10 |
|
Таблица VIII-1 |
|
xn – Расстояние до пунктов
U – Скорость звука
t – Время прибытия самолета в пункт
t' – Время фиксации прибытия самолета в каждый пункт, т.е. кажущееся время прибытия самолета в каждый пункт
Итак, какое расстояние между пунктами вам было известно еще до этого, вычисляете, что самолет перемещался из одного пункта в другой со скоростью:
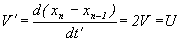
или же:
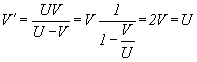
Т.е. в два раза больше реальной. Получается заметный сдвиг между реальной и фиксируемой скоростью.
Вычислим обратную, т.е. для случая удаления:
| x |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.00 |
00.03 |
00.06 |
00.09 |
00.12 |
00.15 |
| Формула: |
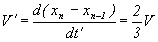 |
|
| или же: |
|
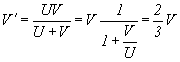 |
| |
| Таблица VIII-2 |
|
Асимметрия в одной и той же скорости для случая сближения и удаления!
Вычислим обратную: Предположим, стоит самолет, а двигается весь аэродром с той же относительной скоростью. Получается следующая панорама:
| Для случая удаления: |
| x |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
| (x-x0)/c |
0 |
1 |
2 |
3 |
4 |
5 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.00 |
00.03 |
00.06 |
00.09 |
00.12 |
00.15 |
|
Формула: |
|
|
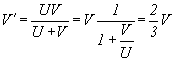
|
| |
| Для случая сближения: |
|
| x |
x5 |
x4 |
x3 |
x2 |
x1 |
x0 |
| (x–x0)/c |
5 |
4 |
3 |
2 |
1 |
0 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.05 |
00.06 |
00.07 |
00.08 |
00.09 |
00.10 |
|
Формула: |
|
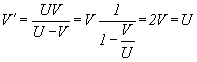 |
|
|
|
Таблица VIII-3 |
|
Для случая: y'≠y или z'≠z, т.е. при угловом наблюдении (см. Рисунок VIII-1 и Таблица VIII-4) получается:
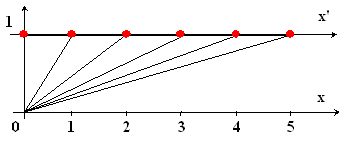
Рисунок VIII-1
По теореме Пифагора [(x'-x0) 2=(x')2+y2] получается:
| Для случая удаления: |
| (x'–x'0)/U |
0 |
1 |
2 |
3 |
4 |
5 |
|
(x'-x0)/U |
1 |
√2 |
√5 |
√10 |
√17 |
√26 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.01 |
00.02+√2 |
00.04+√5 |
00.06+√10 |
00.08+√17 |
00.10+√26 |
| |
Для случая сближения: |
| (x'–x'0)/U |
5 |
4 |
3 |
2 |
1 |
0 |
| (x'–x0)/U |
√26 |
√17 |
√10 |
√5 |
√2 |
1 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.00+√26 |
00.02+√17 |
00.04+√10 |
00.06+√5 |
00.08+√2 |
11 |
| |
|
Таблица VIII-5 |
x'-x0 – расстояние до объекта
t – Реальное время прибытия
t'– Время фиксации прибытия
Обобщая все это можно написать так:
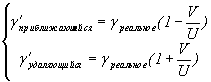
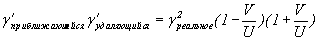
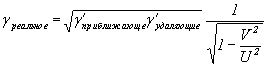
Формула VIII-1
Мы намерены превратить это положение в предпосылку для построения нового подхода. Ниже вычисляем все эффекты, полученные при движении тел со сверхвысокими скоростями, основанные на вышеуказанный пример:
Итак, по принципу дальнодействия:
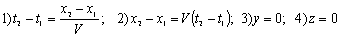
А при принципе близкодействии запаздывание сигналов сюда накладывает свои отпечатки, а именно:
1) Происшествие в точке xn наблюдается в точке x0 не сразу, а именно через 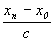 время, т.е.: время, т.е.:
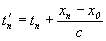
2) Видимое местонахождение (координат) движущегося предмета будет:
xn'= xn ± c (tn' – t0)
где (t'n – t'0) отрезок времени для дохождения сигнала до наблюдателя, т.е. реальное время проделанного расстояния xn – x0
3) Реальное расстояние до движущегося предмета:
x – x0 = (x' – x0) ± (x' – x0)V/с=(x' – x0)(1+V/с);
4) Видимая длительность событий t’2 и t’1, т.е. проекция отрезка времени будет (см: Рис. 1):
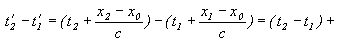
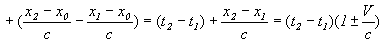
Знак “±” перед V, получается при x2 < x1
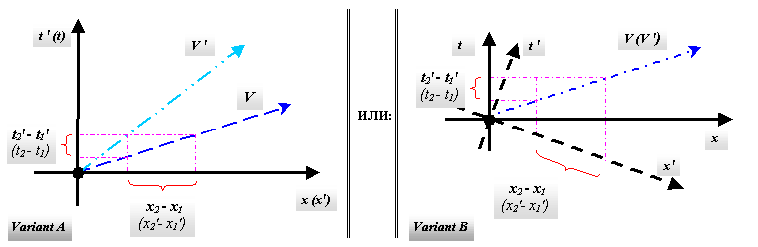
Рисунок 1.
5) Видимая длина предмета, т.е. фиксированное в одно время расстояние между двумя точками движущегося предмета в пункте наблюдения :
x2 – x1 = (x2' – x0)(1+V/с) – (x1' – x0)(1+V/с) = (x2' – x1')(1 ± V/c)
Знак “±” перед V, получается при x2 < x1
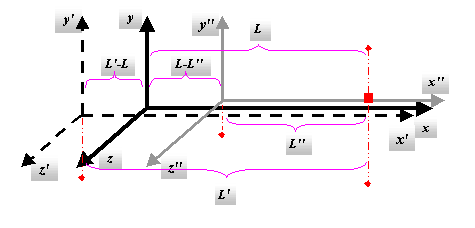
Рисунок 2.
Дополнительно: Допплера эффект об этой растяжке дает более наглядное представление. Т.к. это то же самое изменение в отрезке, которое происходит между двумя фронтами волн при движении источника. Только здесь в обратном порядке.
Итого:
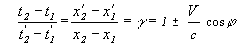
и если раздельно:
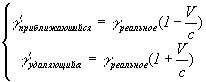
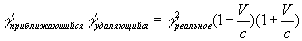
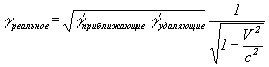
Формула VIII-2
γ – величина, которую можно заменить любым из перечисленных параметров тел – массой, энергией, координатой и т.д., для получения релятивистических величин
t=реальное время события
t'= фиксируемое время события;
t1=время, когда предмет находился в точке x1
t2=время, когда предмет находился в точке x2
x=реальное местонахождение точки
x'=видимое местонахождение точки в данный момент, который в действительности по причине своего движения находится уже не там
x0=местонахождение наблюдателя
(Из-за того, что при необходимости cos φ меняет знак этого V/c, в действительности вообще можно было не писать “±” перед V/c. Во всяком случае речь идет о линейном движении).
Это то же самое “Преобразование Лоренца” – безо всяких допущений. Только в правой части уравнения, в отличие от Лоренца и Эйнштейна варианта, под корнем здесь фигурирует γ 'приближаюшиеся * γ 'удаляющейся, потому, что в отличие от Эйнштейна и Лоренца здесь эти величины отличаются друг от друга. Если бы принимались равными, как у них тогда на месте их обоих остался бы один “ γ ' ”, причем без корня.
7) Одним из самых ценных выводов из этих формул является следующий:
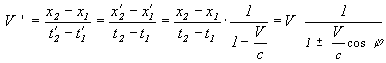
Формула VIII-3
Мы называем эту формулу “формула расщепления скоростей”. Это именно та ситуация, которую иллюстрировали в первых же абзацах этой главы относительно самолета и звука. Она подтверждается в астрономических наблюдениях, т.к. сегодня науке известно около 10-ти квазаров или части квазаров, которые двигаются со скоростью в несколько раз больше световой, например квазар “3С279” (см. 10 стр. 448; 169;...). Наука считает эту сверхсветовую скорость “кажущейся скоростью”. Но, где у Эйнштейна идет речь о кажущихся скоростях, тем более, где ее место в СТО?
Результаты расчетов можно проверить очень легко, подменив везде скорости света на скорость звука, т.е. под величиной “c” подразумевая скорость звука. И поэтому скорость предмета должна быть меньше скорости звука в воздухе, и приборы должны оперировать только со звуковыми сигналами.
Из формулы [Формула VIII-3] легче найти реальную V:
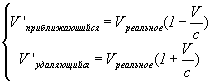
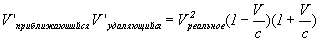
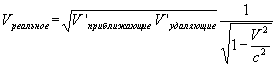
Из вышеизложенных вычислений получаются некоторые интересные результаты, в том числе получается, что:
1) V ' ≠ V ;
2) Если V >0,5c тогда V' >c;
3) Для большинства тензоров первого и второго порядка получается, что:
a) 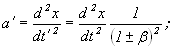
b) 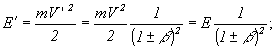
c) 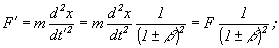
d) 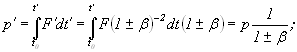
e) 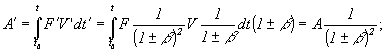
...И т.д... (здесь β=V/c)
4) Относительно “эффекта Хаббла” (т.е. теории “Bigbang”а или расширения Галактик) получается более интересный результат:
Допустим, к нам приближается 10 объектов, расположенных друг от друга на расстоянии xn–x(n-1)=ct, со скоростью V, где V=1/2c, и столько же объектов удаляется от нас. При начале отсчета, каждая удаляющаяся и приближающаяся пара расположена параллельно, т.е. на одной линии и на одинаковой удаленности от точки отсчета (т.е. пространство является однородным; см. Рисунок VIII-2).
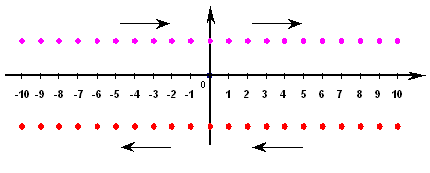
Рисунок VIII-2
Реальное положение движущихся объектов
Учитывая, что мы фиксируем каждый из них не сразу, а именно со сдвигом 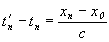 (где индекс n обозначает номер объекта, t - реальное прибытие объекта On в точку xn, t'=фиксируемое время нахождения объекта в точке xn), тогда первые – удаляющиеся и приближающиеся фиксируем через одну секунду, остальные поочередно через каждые 1·n секунд. Итого, последнюю приближающуюся фиксируем через 10 секунд, или же (где индекс n обозначает номер объекта, t - реальное прибытие объекта On в точку xn, t'=фиксируемое время нахождения объекта в точке xn), тогда первые – удаляющиеся и приближающиеся фиксируем через одну секунду, остальные поочередно через каждые 1·n секунд. Итого, последнюю приближающуюся фиксируем через 10 секунд, или же 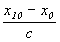 секунд. За это время приближающийся последний приблизится к нам на одну из двух частей общего расстояния или же ровно на (x10–x0)/(1 – V/c), и удаляющийся удалится на столько же. И 5-й из приближающихся, т.е. объект номер O5 будет уже в точке x0, и из удаляющихся то же самое – объект номер O-5 будет в нулевой точке, а стоящие впереди него объекты пересекут границу. Итак, ровно в 00.10 мы фиксируем 5 приближающихся, и всех удаляющихся от нас объектов, и... дополнительно тех, которые за эти 10 секунд “рождались”, т.е. пересекли начале координат и начали удаляться от нас. Учитывая скорости V=1/2c, мы фиксируем за эти 10 секунд еще 5 или же N·(1 – V/c) “новорожденных”. Итого, в нашем распоряжении будет информация о 15-ти удаляющихся, и о 5 приближающихся объектах (Рисунок VIII-3). секунд. За это время приближающийся последний приблизится к нам на одну из двух частей общего расстояния или же ровно на (x10–x0)/(1 – V/c), и удаляющийся удалится на столько же. И 5-й из приближающихся, т.е. объект номер O5 будет уже в точке x0, и из удаляющихся то же самое – объект номер O-5 будет в нулевой точке, а стоящие впереди него объекты пересекут границу. Итак, ровно в 00.10 мы фиксируем 5 приближающихся, и всех удаляющихся от нас объектов, и... дополнительно тех, которые за эти 10 секунд “рождались”, т.е. пересекли начале координат и начали удаляться от нас. Учитывая скорости V=1/2c, мы фиксируем за эти 10 секунд еще 5 или же N·(1 – V/c) “новорожденных”. Итого, в нашем распоряжении будет информация о 15-ти удаляющихся, и о 5 приближающихся объектах (Рисунок VIII-3).
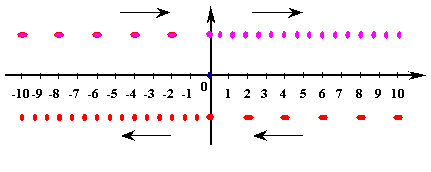
Рисунок VIII-3
Видимое положение удаляющихся и приближающихся объектов
Приняв пространство и время приблизительно однородными, т.е. число удаляющихся и приближающихся, а также вымирающих и новорожденных приблизительно равными и пространственно-временное расстояние между ними тоже, можно вывести общую формулу для количества фиксируемых движущихся объектов, в конкретном n ряде пространства, за конкретное ∆t время:
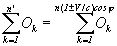
где O – объекты; n – реальное количество объектов, расположенных на равном расстоянии друг от друга (включая и того, который находится в начале координат), и движущихся равномерно относительно начала координат; n' – одновременно фиксируемое количество их в начале координат; знак плюс и минус впереди J – векторная ориентация этих объектов: удаление или приближение их от начала координат; “cos φ” – угол движения относительно систем отсчета.
Итак, получается, что количество приближающихся всегда меньше удаляющихся (в действительности же просто приближающиеся попадают в поле видимости в (1+V/c)/(1-V/c) раз чаще, чем удаляющиеся).
Другое объяснение: Из-за выведенных выше формул скорости и длин, получается, что скорости и расстояние между двумя отрезками точек приближающихся объектов всегда больше удаляющихся ровно на полученный нами коэффициент. Отсюда следует, что и перерыв между последовательно расположенными объектами будет больше или меньше в зависимости от их вектора движения. Получается, что фиксируемая плотность приближающихся веществ во вселенной всегда будет меньше удаляющихся, а именно на 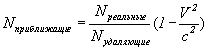 раз. раз.
Тут еще одна деталь: Такое впечатление, что наша модель утверждает линейную разбеганию галактик. Но эта поспешный вывод. Обращайте внимания на этот нюанс: объект приближается к пункту наблюдение со скоростью U=2V, но удаляется со скоростью U=V/2. Однако, такое изменение происходить не скачкообразно. Именно, этот промежуток и добавляет сюда, нужных коэффициент (см. Рисунок 6):
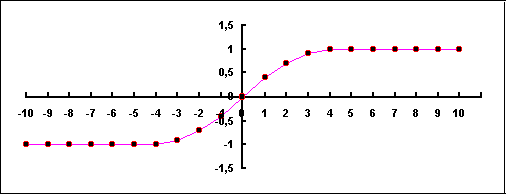
Рисунок VIII-3_1
[Геометрия ускорения галактик]
При вычислений получаем, что скорость увеличивается с расстоянием. Эта вроде «эффект линзы» – чем дальше от точка отчета, тем больше расхождения между реальной и видимой скоростью и координатою.
Но это пока не все. Эти вычисления относились только к случаю пространственной однородности. Временная однородность накладывает на видимое количество объектов во вселенной дополнительный отпечаток. Так как (см. Таблица VIII-6):
Для случая приближения |
| x |
x2 |
x1 |
| t |
00.00 |
00.02 |
| t' |
00.02 |
00.03 |
| Формула: ∆ t'= ∆ t (1-V/c) |
| |
Для случая удаления |
| x |
x1 |
x2 |
| t |
00.00 |
00.02 |
| t' |
00.01 |
00.04 |
Формула: ∆ t'= ∆ t (1+V/c) |
| |
| Таблица VIII-6 |
Здесь:
x1, x2 – координаты, где объект рождался или умер
∆t – реальная длительность жизни объекта
∆t'– кажущаяся длительность жизни объекта
V=1/2c
Получается, что фиксируемая жизнь удаляющихся, длиннее чем приближающихся. В результате опять градиенты плотности для удаляющихся и приближающихся отличаются друг от друга, во столько же раз:
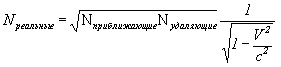
Формула VIII-4
Суммируя оба фактора, для градиента плотности всего пространство-временного континуума получаем:
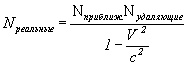
Формула VIII-5
И так, некоторые выводы из [Формула VIII-5]:
Расширение вселенной не более чем оптическая иллюзия, обусловленная принципом близкодействия. Это кажущееся расширение, а не действительное. Реальная стационарность вселенной в любом варианте проецируется на человеческие восприятия динамичным;
Плотность пространственно-временного континуума в действительности отличается от ныне фиксируемого как раз 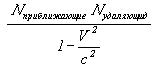 раз;. раз;.
По требованиям Формула VIII-5 энтропия вселенной в действительности 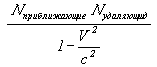 раз меньше чем фиксируется. раз меньше чем фиксируется.
Наши расчеты подтверждается в астрономических наблюдениях, т.к. сегодня науке известно около 10-ти квазаров или части квазаров, которые двигаются со скоростью в несколько раз больше световой, например квазар «ЗС279» (см. 5; 7 стр. 448;...). Наука считает эту сверхсветовую скорость «кажущейся скоростью». Но, в современной релятивистике о кажущихся скоростях не говорится.
А также, релятивистические преобразований параметров тел, при больших скоростях за 100 лет не нашел достаточно обоснованных экспериментальных подтверждений. Т.е. сегодня за релят. преобразование времени науку известен всего – один, за релят. преобразование массы и энергии – 2, за релят. преобразование длины – не один экспериментальных фактов, причем, сегодня и те факты имеют несколько интерпретацию в рамках разных теорий (см. 4).
Литература
1. Mammadov C.M.: A Eynsteynin Xususi Nisbilik Nazariyyasina qeyri-ananavi bax?s. ~B.: «Elm», 1999
2. Логунов А.А.: Лекции по ТО. Совр. анализ проблемы. 2-е изд. ~М.: МГУ 1984
3. Лоренц Г.А.: Теория электронов и ее применение для явлений света. ~М.: Гос. издат. техн.-теор. лит., 1953
4. Мамедов Дж.М.: Заметки и замечания, относительно ряда базовых принципов современной физической науки. ~Б. «Элм»,1999; Б.«Закиоглы»,2005 (в интернете: http://j-m-mamedov.narod.ru/russian/phizic/to_ru.zip, http://ww.phillaw.aznet.org/monru/bigbang_ru.htm)
5. Файнгольд М.: Сверхсветовая тень и взрывающиеся квазары. Журнал «Квант» 1991 №12 (В интернете: http://kvant.mirror0.mccme.ru/1991/12/sverhsvetovaya_ten_i_vzryvayus.htm)
6. Фейнман Р., Лейтон Р., Сендс М.: Фейнмановские лекции по физике. Пер. с анг. т. 6. ~М.: «Мир», 1977
7. Физическая энциклопедия. т. IV. ~М.: Научное изд. «Большая Российская Энциклопедия», 1994
8. Эйнштейн А.: Собр. научн. тр. т. I. ~М.: 1965
|
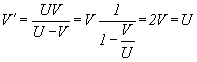
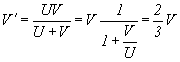
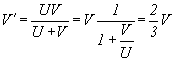

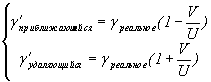
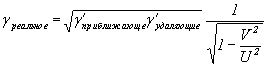


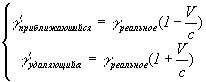
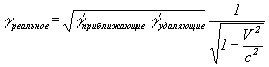
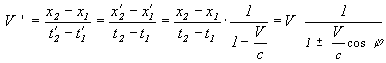
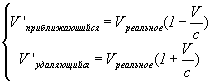
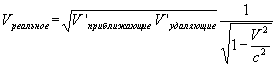
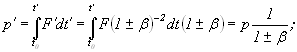
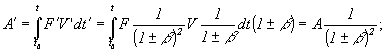


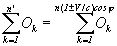

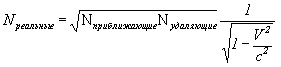
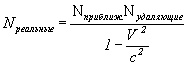
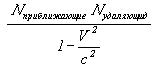 раз;.
раз;.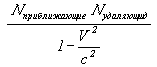 раз меньше чем фиксируется.
раз меньше чем фиксируется.