Мамедов Джаббар Манаф оглы
[Азербайджан]
О НОВОЙ СТРАННОЙ РЕЛЯТИВИСТСКОЙ ЯВЛЕНИИ
|
ИЗДАТЕЛИ:
|
Работа является отрывком из книги автора “Заметки и замечания, относительно ряда базовых принципов современной физической науки”, Баку, 1999, пер. на русскую Баку, 2005; см.: 4;
Журнал “Знание”, Серия “Технические науки” №1, Баку, 2005
|
|
РЕЦЕНЗЕНТЫ
|
Факультет Физики Азерб.Гос.Пед.Университета
Некоторые индивидуальные рецензий
|
|
СКАЧАТЬ
|
Скачать только эту часть
Скачать всю работу
|
|
АДРЕС МАТЕРИАЛА В ИНТЕРНЕТЕ
|
http://www.phillaw.aznet.org/monru/physic/bigbang_ru.htm
http://j-m-mamedov.narod.ru/russian/physic/bigbang_ru.htm
|
|
ФОРУМ, ГДЕ ОБСУЖДАЕТСЯ ЭТА РАБОТА
|
http://www.astronomy.ru/forum/index.phr/topic,10650.0.html
|
Представьте самолет, летящий к вам со скоростью V=1/2U, где V – скорость самолета и U – скорость звука. На пути, на равном расстоянии друг от друга расположены, 5 пунктов. Дистанция между ними равна 1Ut, т.е. столько, сколько звук преодолевает за одну секунду. Итого последний находится на расстоянии 5Ut от вас. Допустим, вы определяете время прибытия самолета в каждый пункт через звуковой сигнал, отправленный из него при прибытии в каждый пункт. Время прибытия и время фиксации этого прибытия будет таким:
| x |
x5 |
x4 |
x3 |
x2 |
x1 |
x0 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.05 |
00.06 |
00.07 |
00.08 |
00.09 |
00.10 |
|
Таблица VIII-1 |
|
xn – Расстояние до пунктов
U – Скорость звука
t – Время прибытия самолета в пункт
t' – Время фиксации прибытия самолета в каждый пункт, т.е. кажущееся время прибытия самолета в каждый пункт
Итак, какое расстояние между пунктами вам было известно еще до этого, вычисляете, что самолет перемещался из одного пункта в другой со скоростью:
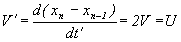
или же:
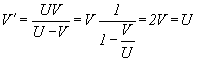
Т.е. в два раза больше реальной. Получается заметный сдвиг между реальной и фиксируемой скоростью.
Вычислим обратную, т.е. для случая удаления:
| x |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.00 |
00.03 |
00.06 |
00.09 |
00.12 |
00.15 |
| Формула: |
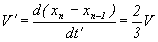 |
|
| или же: |
|
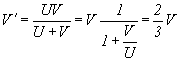 |
| |
| Таблица VIII-2 |
|
Асимметрия в одной и той же скорости для случая сближения и удаления!
Вычислим обратную: Предположим, стоит самолет, а двигается весь аэродром с той же относительной скоростью. Получается следующая панорама:
| Для случая удаления: |
| x |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
| (x-x0)/c |
0 |
1 |
2 |
3 |
4 |
5 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.00 |
00.03 |
00.06 |
00.09 |
00.12 |
00.15 |
|
Формула: |
|
|
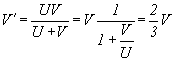
|
| |
| Для случая сближения: |
|
| x |
x5 |
x4 |
x3 |
x2 |
x1 |
x0 |
| (x–x0)/c |
5 |
4 |
3 |
2 |
1 |
0 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.05 |
00.06 |
00.07 |
00.08 |
00.09 |
00.10 |
|
Формула: |
|
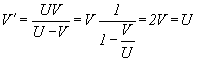 |
|
|
|
Таблица VIII-3 |
|
Для случая: y'≠y или z'≠z, т.е. при угловом наблюдении (см. Рисунок VIII-1 и Таблица VIII-4) получается:
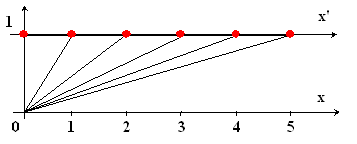
Рисунок VIII-1
По теореме Пифагора [(x'-x0)²=(x')²;+y²] получается:
| Для случая удаления: |
| (x'–x'0)/U |
0 |
1 |
2 |
3 |
4 |
5 |
|
(x'-x0)/U |
1 |
√2 |
√5 |
√10 |
√17 |
√26 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.01 |
00.02+√2 |
00.04+√5 |
00.06+√10 |
00.08+√17 |
00.10+√26 |
| |
Для случая сближения: |
| (x'–x'0)/U |
5 |
4 |
3 |
2 |
1 |
0 |
| (x'–x0)/U |
√26 |
√17 |
√10 |
√5 |
√2 |
1 |
| t |
00.00 |
00.02 |
00.04 |
00.06 |
00.08 |
00.10 |
| t' |
00.00+√26 |
00.02+√17 |
00.04+√10 |
00.06+√5 |
00.08+√2 |
11 |
| |
|
Таблица VIII-5 |
x'-x0 – расстояние до объекта
t – Реальное время прибытия
t' – Время фиксации прибытия
Обобщая все это можно написать так:
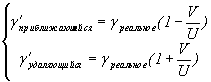
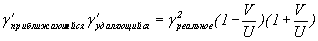
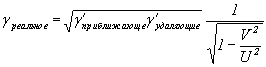
Формула VIII-1
© Мы намерены превратить это положение в предпосылку для построения нового подхода. Ниже вычисляем все эффекты, полученные при движении тел со сверхвысокими скоростями, основанные на вышеуказанный пример:
Итак, по принципу дальнодействия:
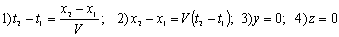
А при принципе близкодействии запаздывание сигналов сюда накладывает свои отпечатки, а именно:
1) Происшествие в точке xn наблюдается в точке x0 не сразу, а именно через 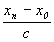 время, т.е.: время, т.е.:
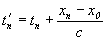
2) Видимое местонахождение (координат) движущегося предмета будет:
xn'= xn ± c (tn ' – t0)
где (t'n – t'0) отрезок времени для дохождения сигнала до наблюдателя, т.е. реальное время проделанного расстояния xn - x0
3) Реальное расстояние до движущегося предмета:
x – x0 = (x' - x0) ± (x' - x0)V/с=(x' – x0)(1+V/с);
4) Видимая длительность событий t’2 и t’1, т.е. проекция отрезка времени будет (см: Рис. 1):
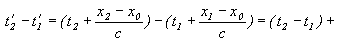
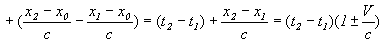
Знак “±” перед V, получается при x2 < x1
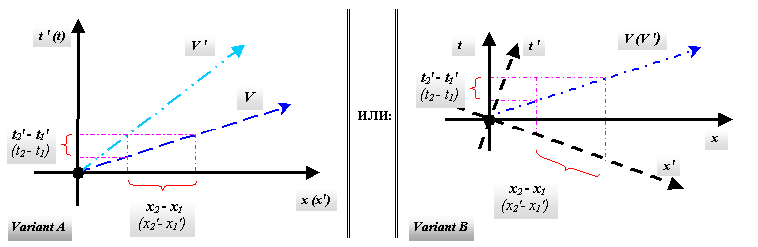
Рисунок 1.
5) Видимая длина предмета, т.е. фиксированное в одно время расстояние между двумя точками движущегося предмета в пункте наблюдения :
x2 - x1 = (x2' – x0)(1+V/с) - (x1' - x0)(1+V/с) = (x2' - x1')(1 ± V/c)
Знак “±” перед V, получается при x2 < x1
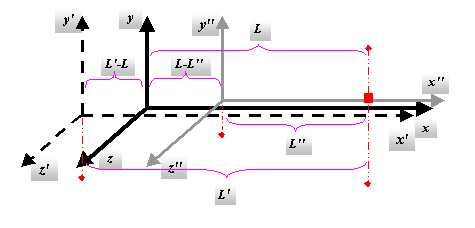
Рисунок 2.
Дополнительно: Допплера эффект об этой растяжке дает более наглядное представление. Т.к. это то же самое изменение в отрезке, которое происходит между двумя фронтами волн при движении источника. Только здесь в обратном порядке.
Итого:
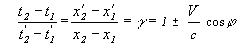
и если раздельно:
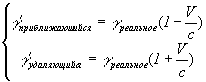
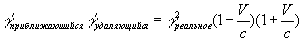
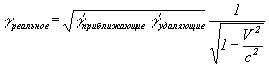
Формула VIII-2
γ – величина, которую можно заменить любым из перечисленных параметров тел – массой, энергией, координатой и т.д., для получения релятивистических величин
t=реальное время события
t'= фиксируемое время события;
t1 = время, когда предмет находился в точке x1
t2 = время, когда предмет находился в точке x2
x = реальное местонахождение точки
x' = видимое местонахождение точки в данный момент, который в действительности по причине своего движения находится уже не там
x0 = местонахождение наблюдателя
(Из-за того, что при необходимости cos φ меняет знак этого V/c, в действительности вообще можно было не писать “±” перед V/c. Во всяком случае речь идет о линейном движении).
Это то же самое “Преобразование Лоренца” – безо всяких допущений. Только в правой части уравнения, в отличие от Лоренца и Эйнштейна варианта, под корнем здесь фигурирует γ 'приближаюшиеся * γ 'удаляющейся, потому, что в отличие от Эйнштейна и Лоренца здесь эти величины отличаются друг от друга. Если бы принимались равными, как у них тогда на месте их обоих остался бы один “ γ ' ”, причем без корня.
7) Одним из самых ценных выводов из этих формул является следующий:
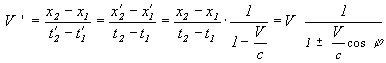
Формула VIII-3
Мы называем эту формулу “формула расщепления скоростей”. Это именно та ситуация, которую иллюстрировали в первых же абзацах этой главы относительно самолета и звука. Она подтверждается в астрономических наблюдениях, т.к. сегодня науке известно около 10-ти квазаров или части квазаров, которые двигаются со скоростью в несколько раз больше световой, например квазар “3С279” (см. 10 стр. 448; 169;...). Наука считает эту сверхсветовую скорость “кажущейся скоростью”. Но, где у Эйнштейна идет речь о кажущихся скоростях, тем более, где ее место в СТО?
Результаты расчетов можно проверить очень легко, подменив везде скорости света на скорость звука, т.е. под величиной “c” подразумевая скорость звука. И поэтому скорость предмета должна быть меньше скорости звука в воздухе, и приборы должны оперировать только со звуковыми сигналами.
Из формулы [Формула VIII-3] легче найти реальную V:
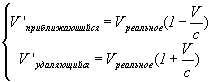
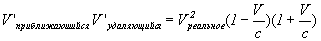
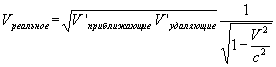
Из вышеизложенных вычислений получаются некоторые интересные результаты, в том числе получается, что:
1) V ' ≠ V;
2) Если V 0,5 c тогда V ' > c;
3) Для большинства тензоров первого и второго порядка получается, что:
a) 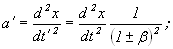
b) 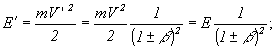
c) 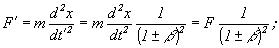
d) 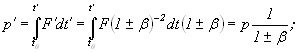
e) 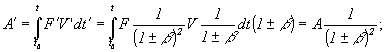
...И т.д... (здесь β=V/c)
4) Относительно плотности и массы вселенной получается более интересный результат:
Допустим, к нам приближается 10 объектов, расположенных друг от друга на расстоянии xn–x(n-1) = ct, со скоростью V, где V = 1/2c, и столько же объектов удаляется от нас. При начале отсчета, каждая удаляющаяся и приближающаяся пара расположена параллельно, т.е. на одной линии и на одинаковой удаленности от точки отсчета (т.е. пространство является однородным; см. Рисунок VIII-2).
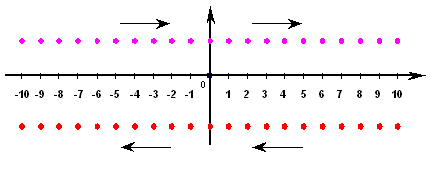
Рисунок VIII-2
Реальное положение движущихся объектов
Учитывая, что мы фиксируем каждый из них не сразу, а именно со сдвигом 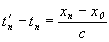 (где индекс n обозначает номер объекта, t - реальное прибытие объекта On в точку xn, t'=фиксируемое время нахождения объекта в точке xn), тогда первые – удаляющиеся и приближающиеся фиксируем через одну секунду, остальные поочередно через каждые 1·n секунд. Итого, последнюю приближающуюся фиксируем через 10 секунд, или же (где индекс n обозначает номер объекта, t - реальное прибытие объекта On в точку xn, t'=фиксируемое время нахождения объекта в точке xn), тогда первые – удаляющиеся и приближающиеся фиксируем через одну секунду, остальные поочередно через каждые 1·n секунд. Итого, последнюю приближающуюся фиксируем через 10 секунд, или же 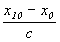 секунд. За это время приближающийся последний приблизится к нам на одну из двух частей общего расстояния или же ровно на (x10–x0)/(1 – V/c), и удаляющийся удалится на столько же. И 5-й из приближающихся, т.е. объект номер O5 будет уже в точке x0, и из удаляющихся то же самое – объект номер O-5 будет в нулевой точке, а стоящие впереди него объекты пересекут границу. Итак, ровно в 00.10 мы фиксируем 5 приближающихся, и всех удаляющихся от нас объектов, и... дополнительно тех, которые за эти 10 секунд “рождались”, т.е. пересекли начале координат и начали удаляться от нас. Учитывая скорости V=1/2c, мы фиксируем за эти 10 секунд еще 5 или же N·(1 - V/c) “новорожденных”. Итого, в нашем распоряжении будет информация о 15-ти удаляющихся, и о 5 приближающихся объектах (Рисунок VIII-3). секунд. За это время приближающийся последний приблизится к нам на одну из двух частей общего расстояния или же ровно на (x10–x0)/(1 – V/c), и удаляющийся удалится на столько же. И 5-й из приближающихся, т.е. объект номер O5 будет уже в точке x0, и из удаляющихся то же самое – объект номер O-5 будет в нулевой точке, а стоящие впереди него объекты пересекут границу. Итак, ровно в 00.10 мы фиксируем 5 приближающихся, и всех удаляющихся от нас объектов, и... дополнительно тех, которые за эти 10 секунд “рождались”, т.е. пересекли начале координат и начали удаляться от нас. Учитывая скорости V=1/2c, мы фиксируем за эти 10 секунд еще 5 или же N·(1 - V/c) “новорожденных”. Итого, в нашем распоряжении будет информация о 15-ти удаляющихся, и о 5 приближающихся объектах (Рисунок VIII-3).
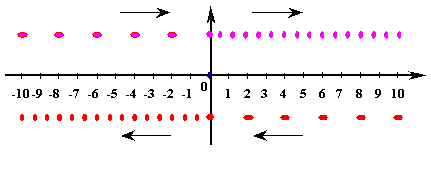
Рисунок VIII-3
Видимое положение удаляющихся и приближающихся объектов
Приняв пространство и время приблизительно однородными, т.е. число удаляющихся и приближающихся, а также вымирающих и новорожденных приблизительно равными и пространственно-временное расстояние между ними тоже, можно вывести общую формулу для количества фиксируемых движущихся объектов, в конкретном n ряде пространства, за конкретное ∆t время:
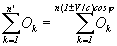
где O – объекты; n – реальное количество объектов, расположенных на равном расстоянии друг от друга (включая и того, который находится в начале координат), и движущихся равномерно относительно начала координат; n' – одновременно фиксируемое количество их в начале координат; знак плюс и минус впереди V – векторная ориентация этих объектов: удаление или приближение их от начала координат; “cos φ” – угол движения относительно систем отсчета.
Итак, получается, что количество приближающихся всегда меньше удаляющихся (в действительности же просто приближающиеся попадают в поле видимости в (1+V/c)/(1-V/c) раз чаще, чем удаляющиеся).
Другое объяснение: Из-за выведенных выше формул скорости и длин, получается, что скорости и расстояние между двумя отрезками точек приближающихся объектов всегда больше удаляющихся ровно на полученный нами коэффициент. Отсюда следует, что и перерыв между последовательно расположенными объектами будет больше или меньше в зависимости от их вектора движения. Получается, что фиксируемая плотность приближающихся веществ во вселенной всегда будет меньше удаляющихся, а именно на 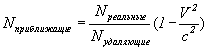 раз. раз.
Тут еще одна деталь: Поскольку, объект приближается к пункту наблюдение со скоростью U = 2V, но удаляется со скоростью U = V/2, отсюда не вытекает, что изменение скорости в точке x ≈ 0 происходить скачкообразно. С приближением расхождение между реальных и фиксируемых скоростей уменьшается, причем не линейно (см. Рисунок 6):
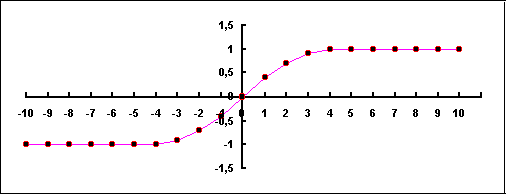
Рисунок VIII-3_1
[Геометрия ускорения галактик]
При вычислений получаем, что скорость увеличивается с расстоянием. Эта вроде «эффект линзы» – чем дальше от точка отчета, тем больше расхождения между реальной и видимой скоростью и координатою.
Но это пока не все. Эти вычисления относились только к случаю пространственной однородности. Временная однородность накладывает на видимое количество объектов во вселенной дополнительный отпечаток. Так как (см. Таблица VIII-6):
Для случая приближения |
| x |
x2 |
x1 |
| t |
00.00 |
00.02 |
| t' |
00.02 |
00.03 |
| Формула: ∆ t'= ∆ t (1-V/c) |
| |
Для случая удаления |
| x |
x1 |
x2 |
| t |
00.00 |
00.02 |
| t' |
00.01 |
00.04 |
|
Формула: ∆ t'= ∆ t (1+V/c) |
| |
| Таблица VIII-6 |
Здесь:
x1, x2 – координаты, где объект рождался или умер
∆ t – реальная длительность жизни объекта
∆ t'– кажущаяся длительность жизни объекта
V = 1/2 c
Получается, что фиксируемая жизнь удаляющихся, длиннее чем приближающихся. В результате опять градиенты плотности для удаляющихся и приближающихся отличаются друг от друга, во столько же раз:
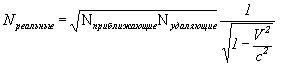
Формула VIII-4
Суммируя оба фактора, для градиента плотности всего пространство-временного континуума получаем:
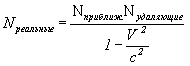
Формула VIII-5
И так, некоторые выводы из [Формула VIII-5]:
При больших скоростях кроме размера, массы и энергии трансформируются (проецируются «искажаются»...) еще и некоторые параметры тел: скорость, ускорение, координаты и т.д., по причине ограниченности предельных скоростей сигналов;
Какую-то часть «эффекта Хаббла» составляет наше явление;
Плотность масса и энтропия пространственно-временного континуума в действительности отличается от ныне фиксируемого как раз 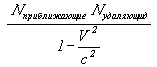 раз; раз;
Этот эффект, возможно, объясняет еще и кое-что на счет «темной материи» («скрытой массы» вселенной);
Наши расчеты подтверждается в астрономических наблюдениях, т.к. сегодня науке известно около 10-ти квазаров или части квазаров, которые двигаются со скоростью в несколько раз больше световой, например квазар «ЗС279» (см. 5; 7 стр. 448;...). Наука считает эту сверхсветовую скорость «кажущейся скоростью». Но, в современной релятивистике о кажущихся скоростях не говорится.
Или же: «В первых экспериментах, поставленных Айвесом (Ives H.) и Стиуллом (Stivell C.) (1), не учитывался знак смещения наблюдаемой частоты. Определялась разностная частота, указывающая только на существование поперечного допплер-эффекта. Но и этот результат был занесен в копилку "подтверждающих СТО" фактов, хотя существование поперечного допплер-эффекта предсказывается и в рамках пострелятивистского подхода [3]. Неопределенность сохранялась до тех пор, пока не были поставлены эксперименты, позволившие определить знак смещения частоты. СТО, как известно, предсказывает "красное смещение" спектра при поперечном эффекте; но эксперименты [2; 7] однозначно указали на его "посинение".»
В конце добавим, что наша версия истинно при той допущении, что свет обязательно привязан к какой-то среде, является возбуждением ее. Появление и распространение света без этой среды невозможно. Эту допущению мы детально анализировали в своей отдельной работе (), и в разных форумах по этой проблеме (), получили одобрение специалистов. Здесь коротко излагаем основных своих аргументов, доказывающих эту допущению:
a) скорость света не зависит от скорости источника, что без исключение присуще волнообразным явлениям;
б) свет восстанавливает свою стандартную скорость “c”, после прохождение среду, чья показатель преломление больше, или меньше единицы;
c) Во всех современных американских и русских проектах космической связи, в том числе в известной GPS и ГЛОНАСС, используется т.н. теория MLET – «Модифицированная лоренцевская теория эфира». А здесь при вычислений принимаются наличие светоносной среды и все расчеты проводятся с учетом того, что эта среда составляет оболочку вокруг массивных тел, в том числе Земли (см.: 12; 13; 14);
d) отрицания светоносной среды не имеют достаточных оснований, т.к. эксперименты, отрицающие этого, не охватываю всевозможных вариантов для такого категорического вывода, в т.ч.:
-
Опыт Майкельсона не был проведен в движущейся относительно Земли системе, причем прямолинейно. Т.к. в непрямолинейном варианте опыт уже проведен (Опыт Саньяка), и получен положительный результат;
-
Он недостаточно проверился в Космосе – на грани магнитного и электрического слоя Земли. Т.к. на опытах Морли-Миллера (1904-1905), Миллера (1921-1925), Майкельсона-Пиза-Пирсона (1929) и др., являющимся вариантом опыта Майкельсона, повторенным на высоте (на дирижабле) обнаружена, а на анологичных опытах Пикара-Стахеля (1926), Кеннеди (1926), Иллингворта (1927) и др. не обнаружена светоносная среда. Критики считают вторую линию некорректным потому, что там не была исключена экранизирующая воздействия стен кабины;
-
Не выяснен отношение света к разным полям: Не выяснен, насколько свет связан с электрическим полем, зависит ли от ее наличия, движения, изменения и т.п.? В таком же порядке и с другими полями в отдельности – магнитными, сильными, слабыми, ядерными полями, физическим вакуумом, гравитацией и т.д. Экранизируя, изменяя поочередно характеристику, напряжение, относительное движение каждого из них, наконец-то, можно было бы поставить точку на вопросе, но не сделан до сих пор.
И еще: Не перепутать нашу позицию, со старой эфирной концепцией. Эфир и светоносная среда – эта совсем разные вещи. Что представляет из себя светоносная среда, какова ее природа – эта уже другой вопрос, и мы оставляем его другим. Относительно какой Системе Отсчета она покоится – то же самое; мы предполагаем, что она обязана составлять оболочку вокруг массивных тел, т.к. для этого достаточно, чтобы один из любых ее полевых потенциалов (заряд, масса...) отличался от нуля. Свет распространяется во вселенной, адаптируя свою траекторию и скорость на то сверхмассивное тело, вблизи которого проходит: Скорость складывается со скоростью его поля, траектория становится криволинейной по известной причине (по причине гравитации сверхмассивных тел). В среднем его скорость, исходя из свойств однородности пространства и времени, будет равна известной “c”, т.к. из этого принципа автоматически вытекает равенство средних масс удаляющихся и приближающихся тел, что и обозначает равенство увлекаемости светоносной среды приближающимися и удаляющимися телами. Отсюда и взаимокомпенсация векторов. А на счет, того, что пока науку не удается построит удовлетворенную солитонную модель фотона, это еще не обозначает, что это вообще не будет возможным и в будущем.
Т.е. мы принимаем вопрос о светоносной среды – пока открытым. А с ее окончательным положительным решением и наша версия получает подтверждению.
Литература
- Ives H., Stilwell C.:
// J. Opt. Soc. Amer., 1938. V.28. P.215.
- Mac-Arthur D.:
Test of the Special-Relativist Doppler Formula …// Phys. Lett., 1986, V.56. No. 4.
- Mammadov C.M.:
A Eynsteynin Xususi Nisbilik Nazariyyasina qeyri-ananavi baxis. ~B.: «Elm», 1999
- Логунов А.А.:
Лекции по ТО. Совр. анализ проблемы. 2-е изд. ~М.: МГУ 1984
- Лоренц Г.А.:
Теория электронов и ее применение для явлений света. ~М.: Гос. издат. техн.-теор. лит., 1953
- Мамедов Дж.М.:
Заметки и замечания, относительно ряда базовых принципов современной физической науки. ~Б. «Элм»,1999; Б.«Закиоглы»,2005 (в интернете: http://j-m-mamedov.narod.ru/russian/phizic/to_ru.zip, http://ww.phillaw.aznet.org/monru/bigbang_ru.htm)
- Победоносцев Л.А., Паршин П.Ф.:
Экспериментальное исследование угловой зависимости в эффекте Доплера // Научный журнал РФО, 1992, №1. С.71-79.
- Файнгольд М.:
Сверхсветовая тень и взрывающиеся квазары. Журнал «Квант» 1991 №12 (В интернете: http://kvant.mirror1.mccme.ru/1991/12/sverhsvetovaya_ten_i_vzryvayus.htm)
- Фейнман Р., Лейтон Р., Сендс М.:
Фейнмановские лекции по физике. Пер. с анг. т. 6. ~М.: «Мир», 1977
- Эйнштейн А.:
Собр. научн. тр. т. I. ~М.: 1965
- Физическая энциклопедия.
т. IV. ~М.: Научное изд. «Большая Российская Энциклопедия», 1994
- Эйнштейн А.:
Собр. научн. тр. т. I. ~М.: 1965
- http://www.egtphysics.net/Mechanism/Clock.pdf
- http://www.egtphysics.net/GPS/RelGPS.htm
- http://www.egtphysics.net
|
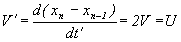
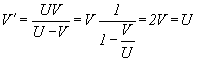
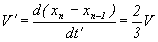
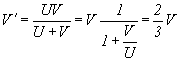
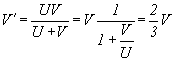

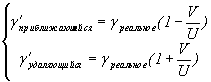
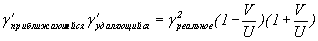
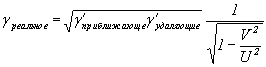
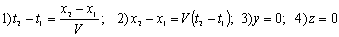
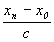 время, т.е.:
время, т.е.: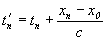
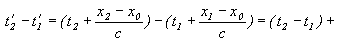
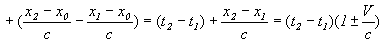


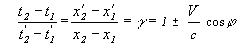
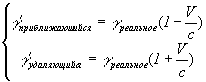
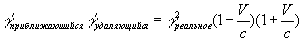
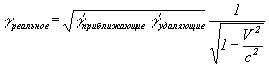
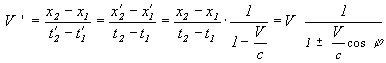
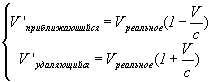
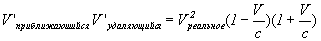
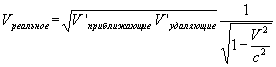
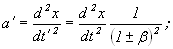
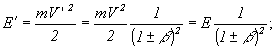
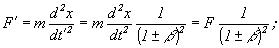
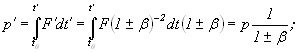
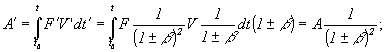

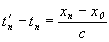 (где индекс n обозначает номер объекта, t - реальное прибытие объекта On в точку xn, t'=фиксируемое время нахождения объекта в точке xn), тогда первые – удаляющиеся и приближающиеся фиксируем через одну секунду, остальные поочередно через каждые 1·n секунд. Итого, последнюю приближающуюся фиксируем через 10 секунд, или же
(где индекс n обозначает номер объекта, t - реальное прибытие объекта On в точку xn, t'=фиксируемое время нахождения объекта в точке xn), тогда первые – удаляющиеся и приближающиеся фиксируем через одну секунду, остальные поочередно через каждые 1·n секунд. Итого, последнюю приближающуюся фиксируем через 10 секунд, или же 
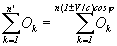
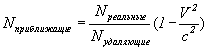 раз.
раз.
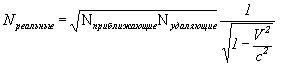
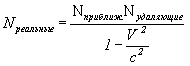
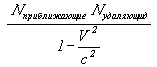 раз;
раз;